Hovedsiden

Innholdsfortegnelse

Kodeeksempler

Løsning på utvalgte oppgaver

Trykkfeilliste

(Nettsiden er under utvikling, mer kommer etter hvert)

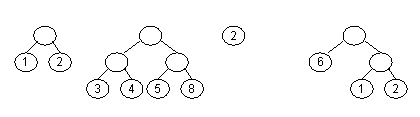
Ei lenket liste kan betraktes som et tre ved å la hodet være rota og hver node ha ett barn.

6.1-4

a) Høyde 1, dybde 2

b) 4 (b, e, f, h)

c) h,f,b,a

d) For eksempel slik:

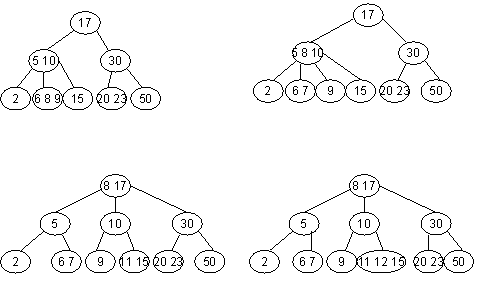
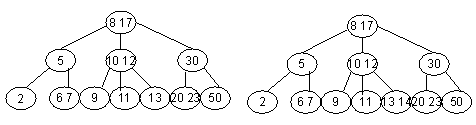
e)

b, c og d kan ordnes på 6 forskjellige måter. I tillegg kan e og f ordnes på 2 måter. Totalt: 12 forskjellige ordnede trær.

6.2-2

C:

  int finnDybde(TreNode* n) {
    if (!n) return -1;
    else return 1 + finnDybde(n->forelder);
  }

Java:

  public int finnDybde(TreNode n) {
    if (n == null) return -1;
    else return 1 + finnDybde(n.forelder);
  }
Dybden kan finnes ved en enkel løkke. Det er bedre enn å bruke rekursjon som gir mange funksjonskall og dermed ekstra bruk av tid og plass i datamaskinen.

6.2-4

Se TreTest.java eller TreTest.c

6.2-6

Postordentraversering. Først sletter vi nodenes etterfølgere, deretter noden selv.

6.3-2

Noen muligheter:
Sortert, f.eks. 3, 5, 8, 11
Omvendt sortert, f.eks. 11, 5, 4, 3
I sikksakk,  f.eks. 11, 3, 5, 4 eller 3, 11, 4, 5

6.3-4

C.

  TreNode* finnNermeste(Tre* t, int nokkel, nokkeltype finnNokkel) {
    TreNode* nermest = NULL;
    int nerhet = INT_MAX;
    TreNode* n = t->rot;
    while (n) {
      int sml = finnNokkel(n->element);
      if (nokkel == sml) return n;
      int test = sml - nokkel;
      if (test < 0) test = -test;
      if (test < nerhet) {
        nermest = n;
        nerhet = test;
      }
      if (nokkel < sml) n = n->venstre;
      else n = n->hoyre;
    }
    return nermest;
  }

Java:

  public TreNode finnNærmeste(int nøkkel) {
    TreNode nærmest = null;
    int nærhet = Integer.MAX_VALUE;
    TreNode n = rot;
    while (n != null) {
      int sml = ((Element)(n.element)).finnNøkkel();
      if (nøkkel == sml) return n;
      if (Math.abs(sml - nøkkel) < nærhet) {
        nærmest = n;
        nærhet = Math.abs(sml - nøkkel);
      }
      if (nøkkel < sml) n = n.venstre;
      else n = n.høyre;
    }
    return nærmest;
  }
 

6.4-1

a) 9

b) 19

c) 29

6.4-3

1 million: ca 2 ms, 1 milliard: ca 3 ms

6.5-1

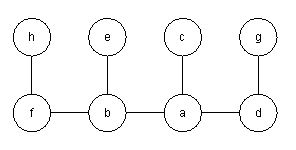
6-1

a)

b)

Fullt binærtre

c), d) e) Se TestBroek.c eller TestBroek.java

f) I d: Postordentraversering. Vi må regne ut verdien på begge barna før vi kan regne ut nodens verdi.
   I e: Inordentraversering. Vi skriver først ut venstre barn, deretter noden (brøkstrek) og til slutt høyre barn,